Droites remarquables, transformations

Sommaire

Ce document rédigé pour les étudiants de la licence scientifique générale (L3 pour des futurs professeurs des écoles à l'université Paris-Sud) accompagne une partie du cours de géométrie basé sur l'ouvrage de Daniel Perrin : Mathématiques d'école : nombres, mesures et géométrie publié par Editions Cassini (402 p. ISBN 978-2-84225-158-1) . On y fait référence par ME.

ME exercice 187, 185 renvoie à l'exercice 187 de la nouvelle édition, 185 de la première. De même pour les pages ou les propositions.
ME VI.1. renvoie à la partie 1 du chapitre 6.

Son but est d'illustrer les révisions du chapitre IV de ME en liant transformations et droites remarquables du triangle. Les premières constructions à la règle et au compas sont établies [ME.VI].

Cas d'isométrie

Si deux triangles sont isométriques (c'est-à-dire s'il existe une isométrie qui envoie l'un sur l'autre), alors leurs angles et leurs côtés homologues sont égaux. On obtient donc 6 égalités. Pour montrer que deux triangles sont isométriques, il suffit de 3 égalités bien choisies. On rappelle ici les trois cas d'isométrie pour les triangles quelconques (pour des énoncés plus précis, voir [ME.IV.4.a]) et on illustre le premier à l'aide de figures mobiles.

Premier cas d'isométrie
Deuxième cas d'isométrie
Troisième cas d'isométrie
Cas d'isométrie des triangles rectangles

Pour une application des cas d'isométrie, voir la démonstration du théorème - définition des polygones convexes réguliers.

Premier cas d'isométrie

Premier cas : Si deux triangles ont un angle égal compris entre deux côtés égaux alors ils sont isométriques.

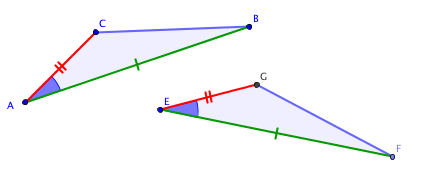
Remarque : Il est essentiel que l'angle égal soit compris entre les deux côtés égaux. Il suffit de regarder cette figure .
Mais ce n'est pas utile pour les triangles rectangles .

Figures mobiles :

Les deux triangles sont directement isométriques.
Les deux triangles sont indirectement isométriques.

Contre-exemple

Les triangles

ABC

ABC'

ont un angle égal et deux côtés égaux mais ils ne sont pas isométriques ; l'aire de

ABC

est strictement plus petite que celle de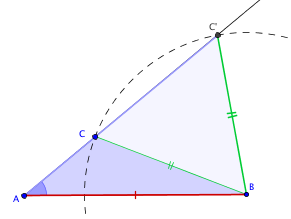

ABC'

figure contre exemple

Les deux triangles sont directement isométriques.

Sur la figure, on voit comment les hypothèses permettent de superposer peu à peu le triangle $A B C$ sur le triangle $E F G$ . On commence par translater $A B C$ pour amener $A$ sur $E$ , puis on fait tourner le triangle autour de $E$ pour superposer $B$ sur $F$ . Alors $C$ est amené en $G$ . Les triangles sont directement isométriques.

Les deux triangles sont indirectement isométriques.

Sur la figure, on voit comment les hypothèses permettent de superposer peu à peu le triangle $A B C$ sur le triangle $E F G$ . On commence par translater $A B C$ pour amener $A$ sur $E$ , puis on fait tourner le triangle autour de $E$ pour superposer $B$ sur $F$ . Ensuite on retourne le triangle selon $(E F)$ (symétrie d'axe $(E F)$ ). Les triangles sont indirectement isométriques.

Deuxième cas d'isométrie

Deuxième cas : Si deux triangles ont deux angles égaux et un côté égal, alors ils sont isométriques.

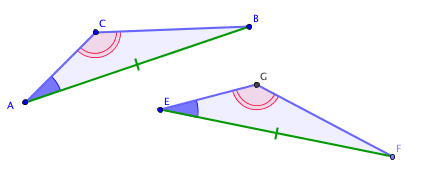
Remarque : Si deux triangles ont deux angles égaux, leurs trois angles sont égaux.

Troisième cas d'isométrie

Troisième cas : Si deux triangles ont leurs trois côtés égaux alors ils sont isométriques.

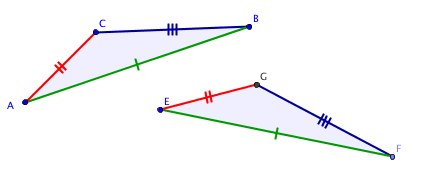
Remarque : Ce cas est très utile pour construire, à l'aide d'un compas, un triangle isométrique à un triangle donné, par exemple, pour reporter un angle.

Cas d'isométrie des triangles rectangles

Cas d'isométrie des triangles rectangles : Si deux triangles rectangles ont deux côtés homologues égaux, alors ils sont isométriques.

Les hypoténuses sont des côtés homologues, les côtés de l'angle droit sont homologues.

Constructions à la règle et au compas (principe)

Ce chapitre comporte un contexte historique et culturel important, lire [ME. VI. Introduction].

Ici sont repris les principes de la construction à la règle et au compas, tels qu'ils sont posés dans [ME.VI.1.A]. Les constructions fondamentales sont établies au moment où les résultats nécessaires sont énoncés.

Soit $𝒫$ $= {M_{1}, . . ., M_{n}}$ un ensemble de $n$ points du plan. On appelle figures constructibles à la règle et au compas à partir de $𝒫$ :

les droites passant par deux points distincts de $𝒫$ ,
les cercles centrés en un point de $𝒫$ passant par un autre point de $𝒫$ .

Définitions : Point constructible à la règle et au compas à partir de $𝒫$ .

On dit qu'un point $M$ est constructible à la règle et au compas en un pas à partir de $𝒫$ s'il est l'intersection de deux figures constructibles à la règle et au compas à partir de .
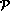On dit qu'un point $M$ est constructible à partir de $𝒫$ si on peut le construit en un nombre fini de pas à partir de $𝒫$ c’est-à-dire, précisément, s’il existe des points $M_{1}$ , $M_{2}$ ,... , $M_{r}$ tels que $M_{r} = M$ et que, pour $i = 1, . . ., r - 1$ , $M_{i + 1}$ est constructible en un pas à partir de $𝒫$ $\cup {M_{1}, . . ., M_{i}}$ .
On dit alors que la construction est faite en $r$ pas.

Comment rédiger un exercice de construction ?

Les deux premières parties ne sont pas le lieu de décrire la construction.

La partie analyse détermine des conditions nécessaires vérifiées par les points à construire. Evidemment pour permettre l'analyse, une figure est nécessaire, on peut tricher pour la faire.
Dans les exercices assez simples, les conditions déterminées par l'analyse sont suffisantes, c'est-à-dire nous assurent que les points ainsi construits répondent au problème. Dans un exercice plus complexe, il faut s'assurer que les points construits satisfont les propriétés demandées. C'est la partie synthèse.
La partie construction est la description précise (mais sans justification) des étapes nécessaires au tracé de la figure. Il peut arriver que la construction ne suive pas le fil de l'analyse. On peut préciser le nombre de pas si cela est demandé ou pour comparer deux constructions.

Parallélogramme

Propriétés caractéristiques du parallélogramme

Soit $A B C D$ un quadrilatère convexe (voir [ME. fig. 20 page 156, fig.5 page 152]). On dit que $A B C D$ est un parallélogramme s'il vérifie l'une des propriétés équivalentes suivantes.

Les côtés opposés sont parallèles.
Les côtés opposés sont de même longueur.
Les côtés $[A B]$ et $[D C]$ sont parallèles et de même longueur.
Les côtés $[A D]$ et $[B C]$ sont parallèles et de même longueur.
Les diagonales $[A C]$ et $[B D]$ se coupent en leur milieu.
$\vec{A B} = \vec{D C}$
$\vec{A D} = \vec{B C}$
$\vec{A B} + \vec{A D} = \vec{A C}$
Les angles opposés sont égaux.

Constructions et parallélogramme

Construction d'un parallélogramme : Les points $A$ , $B$ et $D$ étant donnés, on utilise la propriété 5 pour construire le parallélogramme $A B C D$ [ME. VI.1. e].
De la construction du parallélogramme, on déduit la construction d'une parallèle à une droite donnée passant par un point donné grâce à la propriété 1 [ME.VI.1. e]. Dans la deuxième édition, on trouve une autre construction d'une parallèle .
De la construction du parallélogramme, on déduit le report de longueur grâce à la propriété 2 [ME. VI.1.f].

Démonstrations à l'aide de parallélogrammes

Droite des mileux
Concours des médianes

Construction d'une parallèle en 2 pas

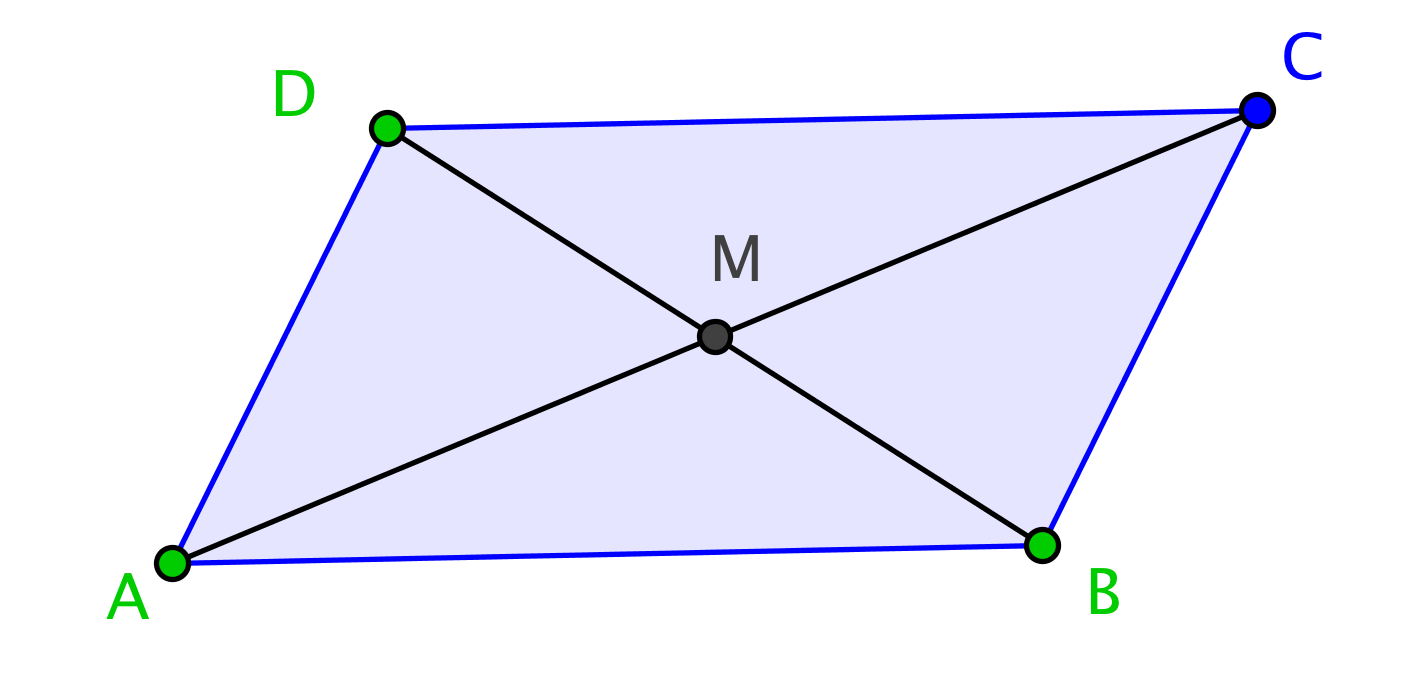
Etant donnés une droite $(AB)$ et un point $C$ extérieur à $(AB)$ , on cherche à construire la parallèle à $(AB)$ passant par $C$ , c'est-à-dire un point $D$ tel que $(CD)$ soit parallèle à $(AB)$ .

L'idée est de construire un triangle $ECD$ tel que $(AB)$ soit une droite des milieux dans le triangle. Il suffit de construire $E$ , le symétrique de $C$ par rapport à $A$ et $D$ , celui de $E$ par rapport à $B$ . La construction est faite en deux pas.

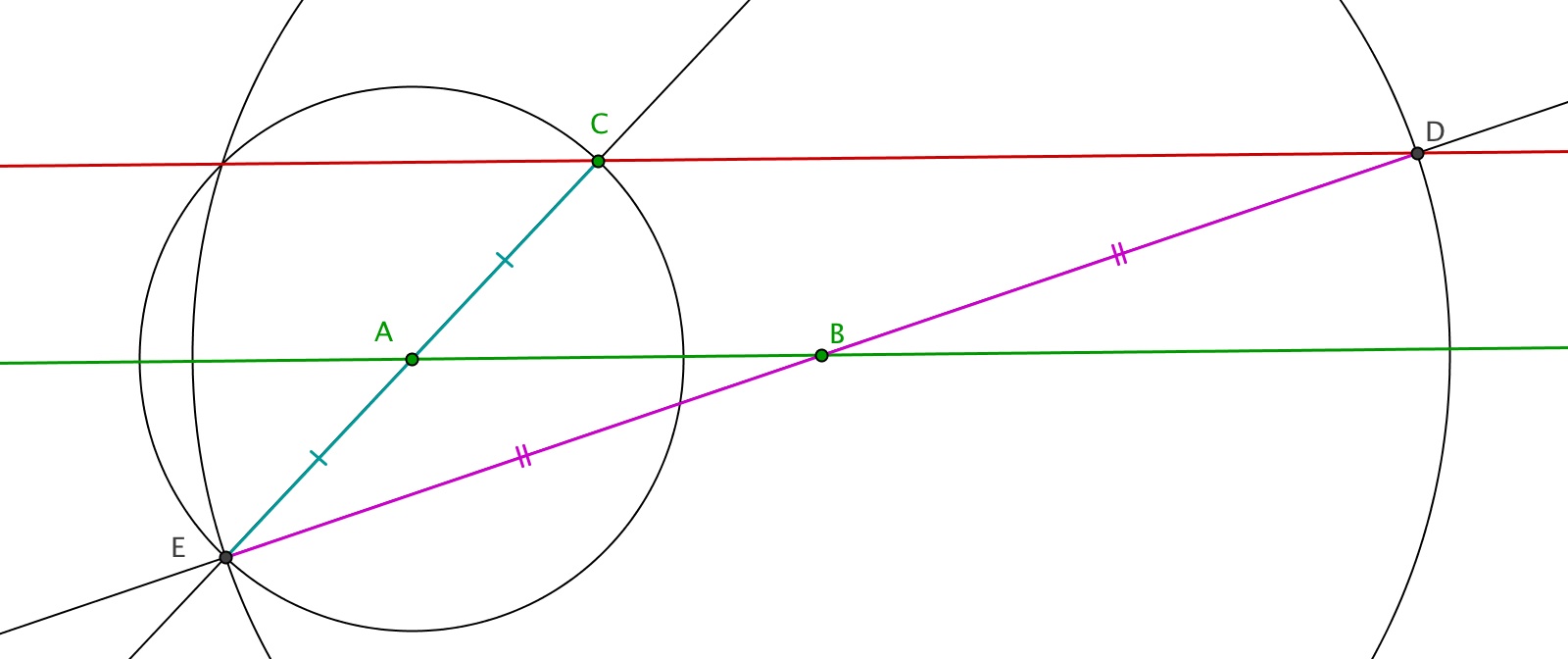
Droite des mileux

Proposition. Soit un triangle

A B C

B'

C'

les milieux respectifs des côtés

[A C]

[A B]

La droite $(B' C')$ , dite droite des milieux, est parallèle à $(BC$ et on a l'égalité : $B' C' = \frac{B C}{2}$ .

Réciproquement, si une droite $𝒟$ passe par $C'$ et est parallèle à $(BC)$ alors elle passe par $B'$ ; c'est la droites de milieux.

Pour dérouler la démonstration de la première affirmation, cliquez sur la flèche..

Soit un triangle $ABC$ et $B'$ et $C'$ les milieux respectifs des côtés $[A C]$ et $[A B]$ .
On s'intéresse à la droite des milieux $(C' B')$ .
Le point $D$ est le symétrique de $C'$ par rapport à $B'$ donc $B'$ est le milieu de $[C' D]$ .
Le quadrilatère $A C' C D$ est un parallélogramme car ses diagonales se coupent en leur milieu.
Comme $A C' C D$ est un parallélogramme, ses cotés $[AC']$ et $[D C]$ sont parallèles et de même longueur.
Comme $C'$ est le milieu de $[A B]$ , on en déduit que les cotés $[B C']$ et $[D C]$ de $B C' D C$ sont parallèles et de même longueur.
Le quadrilatère convexe $B C' D C$ est donc un parallélogramme.
Les côtés $[C' D]$ et $[B C]$ sont parallèles et de même longueur ; la partie directe de la proposition est démontrée.

Pour démontrer la réciproque, on utilise l'unicité de la parallèle à $(B C)$ passant par $C'$ : si une droite $𝒟$ passe par $C'$ et est parallèle à $(BC)$ , c'est nécessairement la droite des milieux donc elle passe par $B'$ .

Translation

Définition. Soit

\overset{⇀}{u}

un vecteur du plan. On appelle translation de vecteur

\overset{⇀}{u}

, notée

t_{\overset{⇀}{u}}

, la transformation du plan qui à un point

M

associe le point

M'

tel que

\vec{M M'} = \overset{⇀}{u}

Des propriétés du parallélogramme, on déduit la construction de l'image d'un point par une translation donnée. En effet, soient $A$ et $B$ deux points distincts ; le point $M'$ est l'image de $M$ par la translation de vecteur $\vec{A B}$ si et seulement si $A B M' M$ est un parallélogramme.

Symétrie orthogonale

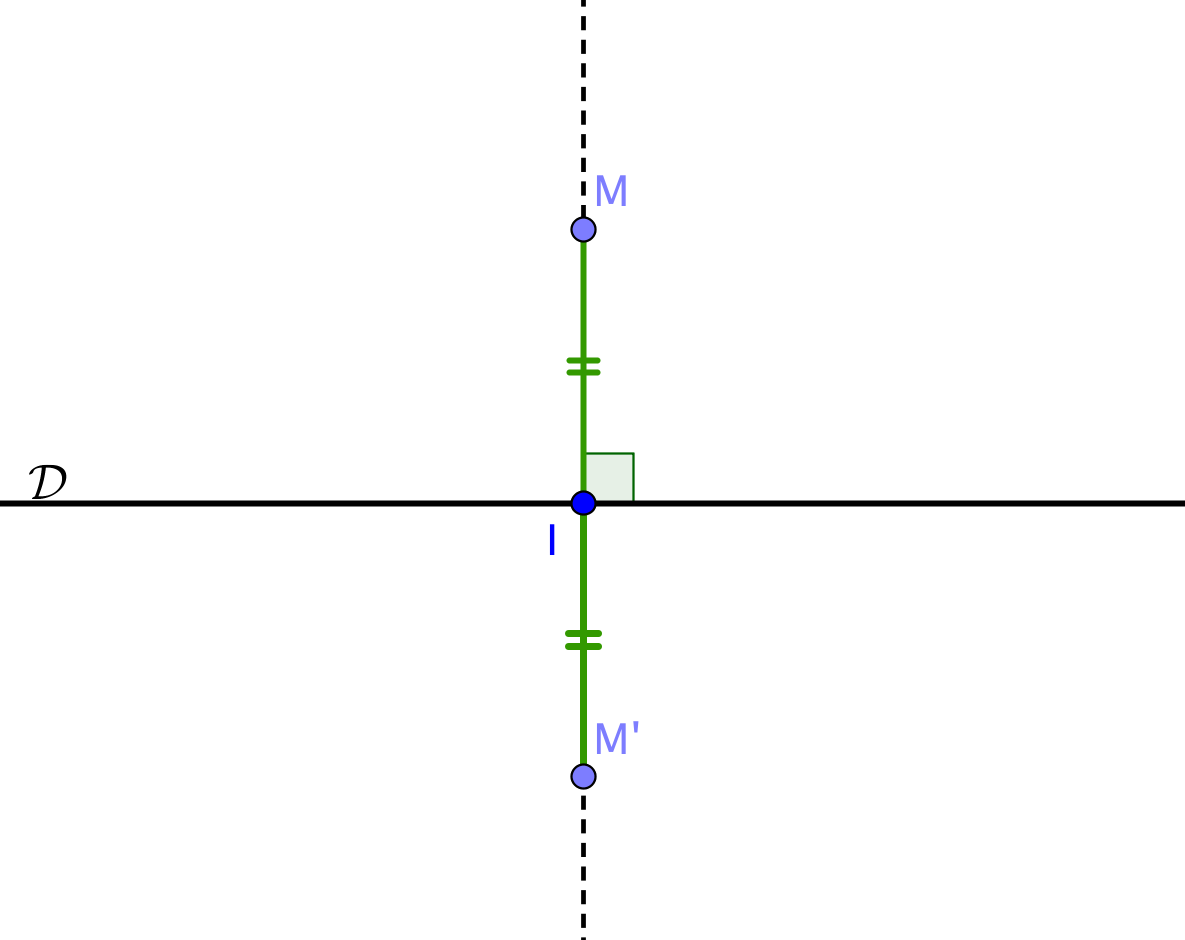
Définition : On appelle symétrie orthogonale d'axe $𝒟$ et on note

s_{𝒟}

la transformation du plan qui à un point

M

associe le point

M'

tel que

la droite $(M M')$ est perpendiculaire à $𝒟$ .
le milieu $I$ de $[M M']$ appartient à $𝒟$ .

Propriétés

La symétrie $s_{𝒟}$ est une isométrie, $s_{𝒟}$ conserve donc les longueurs et les angles géométriques.
L'axe $𝒟$ de $s_{𝒟}$ est l'ensemble de ses points fixes.
$s_{𝒟} \circ s_{𝒟}$ est l'identité, une symétrie est son propre inverse.

Médiatrice d'un segment

Définition : On appelle médiatrice du segment $[B C]$ la droite

𝒟

qui vérifie l'une des propriétés équivalentes suivantes :

$𝒟$ est la perpendiculaire à $(B C)$ en $A'$ , milieu de $[B C]$ .
$𝒟$ est l'ensemble des points équidistants des extrémités de $[B C]$ .
$𝒟$ est l'axe de l'unique réflexion qui échange $B$ et $C$ .

On en déduit le protocole de construction de la médiatrice, du milieu de $[B C]$ et celui d'une perpendiculaire à une droite donnée passant par un point donné .

Proposition : Les médiatrices des côtés d'un triangle sont concourantes en un point

O

, centre du cercle circonscrit au triangle.

Démonstration. Notons $Δ_{A}$ , $Δ_{B}$ et $Δ_{C}$ les médiatrices respectives de $[B C]$ , $[C A]$ et $[A B]$ . Puisque $A$ , $B$ et $C$ ne sont pas alignés, $Δ_{A}$ et $Δ_{B}$ sont sécantes comme perpendiculaires à deux droites non parallèles. Soit $O$ leur point d'intersection. La caractérisation 2 des médiatrices donne les deux égalités : $B O = C O$ et $A O = C O$ . On en déduit que $O$ est équidistant de $A$ et $B$ donc, toujours par la caractérisation 2 des médiatrices, on obtient que $O$ appartient aussi à $Δ_{C}$ . On a démontré que les trois médiatrices sont concourantes en $O$ , point équidistant des trois sommets du triangle, donc centre du cercle passant par les trois sommets du triangle, dit circonscrit au triangle.

Protocole de construction de la médiatrice et du milieu

Les points donnés sont en vert, les objets construits sont en rouge. La construction de la médiatrice se fait en 2 pas, celle du milieu en 3 pas ( voir [ME VI.1.c]). La médiatrice est la droite $(C D)$ où $C$ et $D$ sont les intersections des cercles $𝒞 (A, A B)$ et $𝒞 (B, A B)$ . Le milieu de $[A B]$ est l'intersection de $(A B)$ et $(C D)$ .
Déroulez la construction avec les flèches en bas.

Construction d'une perpendiculaire

On cherche à construire la perpendiculaire à $(A B)$ passant par $C$ . Deux cas se présentent :

Soient $A$ , $B$ et $C$ trois points non alignés. Par définition de $s_{(AB)}$ , la perpendiculaire à $(A B)$ passant par $C$ est la droite $(C C')$ où $C'$ est le symétrique de $C$ par rapport à $(A B)$ .
La construction se fait en un pas : les points $C$ et $C'$ sont les intersections de $𝒞 (A, A C)$ et $𝒞 (B, B C)$ . On a utilisé les propriétés 1 et 2 de la symétrie orthogonale et la propriété M2 de la médiatrice .
Soient $A$ , $B$ et $C$ trois points alignés. Soit $A'$ le symétrique de $A$ par rapport à $C$ , alors $C$ est le milieu de $[A A']$ et la médiatrice de $[A A']$ est la perpendiculaire à $(A B)$ passant par $C$ . La construction se fait en 3 pas.

Homothétie

Définition. [ME.IV.3.e]
Soit

k

un réel différent de

0

et de

1

C

un point du plan. On appelle homothétie de centre $C$ et de rapport $k$ (et on note

h (C, k)

) la transformation du plan qui à un point

M

associe le point

M'

tel que

\vec{C M'} = k . \vec{C M}

On peut formuler le théorème de Thalès [ME.IV.1.e] à l'aide d'une homothétie, c'est parfois plus simple, par exemple dans l' espace .

Homothétie et théorème de Thalès

Soit

(M M')

(P P')

deux droites sécantes en un point

C

. Il existe une homothétie de centre

C

qui envoie

M

sur

M'

P

sur

P'

si et seulement si

(M P)

(M' P')

sont parallèles. Le rapport de l'homothétie est alors :

$k = \frac{\bar{CM'}}{\bar{CM}} = \frac{\bar{C P'}}{\bar{C P}} = \frac{\bar{P' M'}}{\bar{P M}}$ .

Médianes

Soit un triangle $ABC$ . On note $A'$ , $B'$ et $C'$ les milieux respectifs de $[B C]$ , $[C A]$ et $[A B]$ .

Définition : On appelle la droite

(A A')

médiane issue de $A$ dans le triangle $A B C$ .

Proposition : Les médianes de

A B C

sont concourantes en un point

G

appelé centre de gravité de $A B C$ . De plus l'homothétie de centre

G

et de rapport

- \frac{1}{2}

envoie

A

sur

A'

B

sur

B'

C

sur

C'

Démonstration : On peut démontrer le concours des médianes à l'aide de parallélogrammes , des aires ([ME exercice 194, 192]) ou de l' associativité du barycentre.

Soit $G$ l'isobarycentre de $A$ , $B$ et $C$ . Par associativité, $G$ est le barycentre de ${(A, \frac{1}{3}), (A', \frac{2}{3})}$ puisque $A'$ est le barycentre de ${(B, \frac{1}{3}), (C, \frac{1}{3})}$ . Donc $G$ appartient à la médiane $(AA')$ et on a : $\vec{AG} = \frac{2}{3} \vec{AA'}$ $\vec{AG} = \frac{2}{3} \vec{AA'}$ et aussi $\vec{GA'} = - \frac{1}{2} \vec{GA}$ . De même pour les autres médianes.

Remarque : Les triangles $ABC$ et $A' B' C'$ ont même centre de gravité $G$ . En effet, les homothéties conservent les barycentres donc l'image $h (G, - \frac{1}{2}) (G) = G$ de $G$ est l'isobarycentre de $A' B' C'$ .

On peut voir l'homothétie en action dans une démonstration du concours des hauteurs .

Concours des médianes

Voici une démonstration du concours des médianes d'un triangle qui utilise le théorème de la droite des milieux et les propriétés des parallélogrammes . Les points $A'$ , $B'$ et $C'$ sont les milieux respectifs des côtés du triangle $ABC$ .

Pour dérouler la démonstration, cliquez sur la flèche.

Soit un triangle $ABC$ .
Le point $G$ est le point d'intersection des médianes $(BB')$ et $(CC')$ .
Soit $A ″$ le symétrique de $A$ par rapport à $G$ .
Dans $ABA ″$ , $(C' G)$ est une droite des milieux, donc parallèle à $(BA ″)$ .
De même, dans $ACA ″$ , $(B' G)$ est une droite des milieux, donc parallèle à $(CA ″)$ .
On en déduit que les côtés opposés de $BGCA ″$ sont parallèles donc c'est un parallélogramme.
Les diagonales de $BGCA ″$ se coupent en leur milieu, donc $G$ appartient à la médiane $(AA')$ .

Hauteurs

Définition. Soit

A ″

le projeté orthogonal de A sur

(B C)

. On appelle hauteur issue de $A$ dans $A B C$ la droite

(A A ″)

Proposition. Les hauteurs de

A B C

sont concourantes en un point

H

appelé orthocentre du triangle $A B C$ .

De nombreuses démonstrations sont possibles pour cette proposition.

Démonstration avec une homothétie

Le concours des hauteurs se déduit de celui des médiatrices grâce à l'homothétie $h (G, - \frac{1}{2})$ . En effet l'image de $(A A ″)$ par cette homothétie est $Δ_{A}$ , car c'est la droite passant par $A'$ , image de $A$ , et parallèle à $(A A ″)$ donc perpendiculaire à $(B C)$ . Les médiatrices sont concourantes en $O$ donc les hauteurs sont concourantes en $H = h (G, - 2) (O)$ .
Observez la transformation de $O$ en $H$ sur cette autre figure .

Sur la figure, cochez et décochez les deux premières cases pour tester l'homothétie sur les triangles, les deux dernières pour la tester sur la hauteur. Quand le curseur apparaît, vous pouvez faire varier le rapport de l'homothétie.

Relation entre l'orthocentre et le centre du cercle circonscrit

Les hauteurs (en rose) sont envoyées par l'homothétie $h (G, k)$ (quand $k$ atteint $- 0, 5$ ) sur les médiatrices (en bleu). Ainsi $h (G, - 2)$ envoie $O$ , le centre du cercle circonscrit au triangle, point de concours de médiatrices sur un point $H$ qui appartient aux 3 hauteurs.

Bissectrice d'un secteur angulaire, d'un angle

Pour la notion de secteur angulaire et d'angle, voir [ME.IV.1.f.].

Bissectrice d'un secteur [ME.IV.1.j.]

Définition et proposition.

Soit $[\hat{B A C}]$ un secteur angulaire saillant. Il existe une unique droite $Δ$ passant par $A$ , appelée bissectrice du secteur $[\hat{BAC}]$ , telle que les deux demi-droites $[A x)$ et $[A y)$ portées par $Δ$ vérifient :

$\hat{B A x} = \hat{x A C}$ et $\hat{B A y} = \hat{y A C} .$

On appelle bissectrice intérieure du secteur $[\hat{B A C}]$ celle parmi les demi-droites $[A x)$ et $[A y)$ qui est contenue dans $[\hat{B A C}]$ . Dans cette page, on supposera que c'est $[A x)$ .

On dit aussi que $Δ$ est la bissectrice de l'angle $\hat{B A C}$ .

Propriétés de la bissectrice du secteur

La droite $Δ$ est la bissectrice de $[\hat{B A C}]$ si et seulement si $Δ$ est axe de symétrie de $[A B)$ et $[A C)$ .
Soient $B' \in [A B)$ et $C' \in [A C)$ tels que $A B' = A C'$ alors $Δ$ est la bissectrice du secteur si et seulement si $Δ$ est la médiatrice de $[B' C']$ .

Démonstration de la propriété 2 et construction de la bissectrice .

Propriétés de la bissectrice intérieure $[A x)$ du secteur

La demi-droite $[A x)$ partage le secteur $[\hat{B A C}]$ en deux secteurs angulaires saillants de même angle.
La demi-droite $[A x)$ est l'ensemble des points de $[\hat{B A C}]$ équidistants des demi-droites $[A B)$ et $[A C)$ . Démonstration

Construction d'une bissectrice

Propriété 2 de la bissectrice de

\hat{B A C}

: Soient

B' \in [A B)

C' \in [A C)

tels que

A B' = A C'

alors

Δ

est la bissectrice

Δ

\hat{B A C}

si et seulement si

Δ

est la médiatrice de

[B' C']

Démonstration. : Soit $M$ le point d'intersection de $(B' C')$ et de $Δ$ .

Si $Δ$ est la bissectrice de $\hat{B A C}$ , on montre à l'aide du premier cas d'isométrie que les triangles $B' A M$ et $C' A M$ sont isométriques. On en déduit que $M$ est le milieu de $[B' C']$ et que les angles $\hat{A M B'}$ et $\hat{A M C'}$ égaux et supplémentaires sont droits. On a montré que la droite $Δ$ est la médiatrice de $[B' C']$ .

Réciproquement, si $Δ$ est la médiatrice de $[B' C']$ , alors $A$ appartient à $Δ$ et la symétrie d'axe $Δ$ échange $B'$ et $C'$ et fixe $A$ donc elle échange $[AB)$ et $[AC)$ , c'est la bissectrice de $\hat{B A C}$ d'après la propriété 1.

Figure de la partie directe	Figure de la réciproque

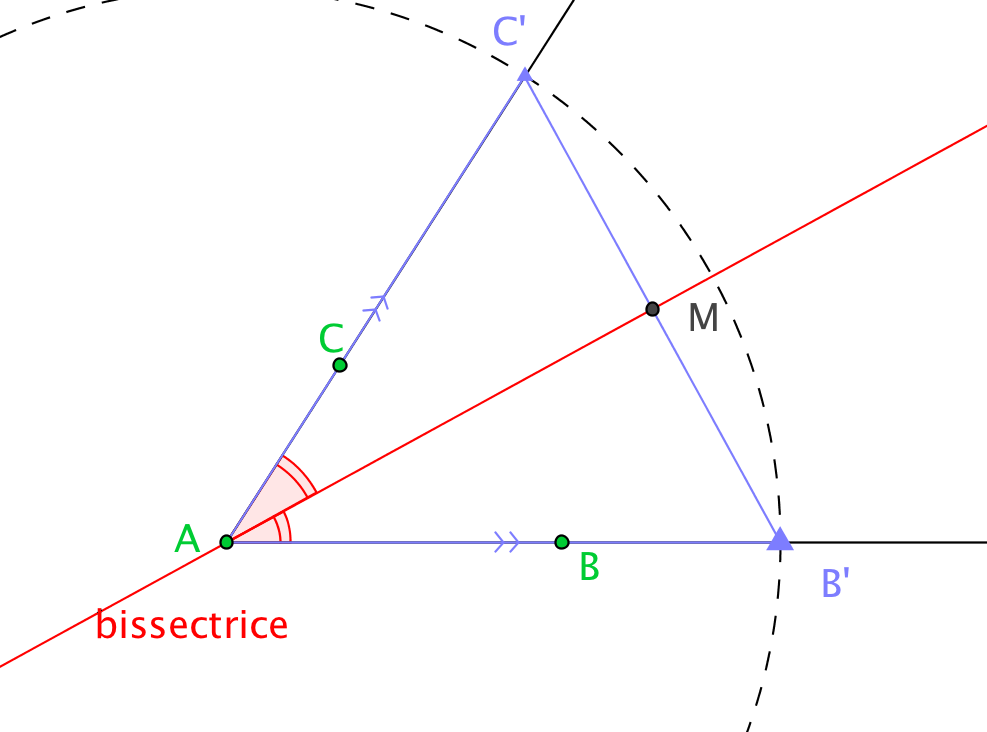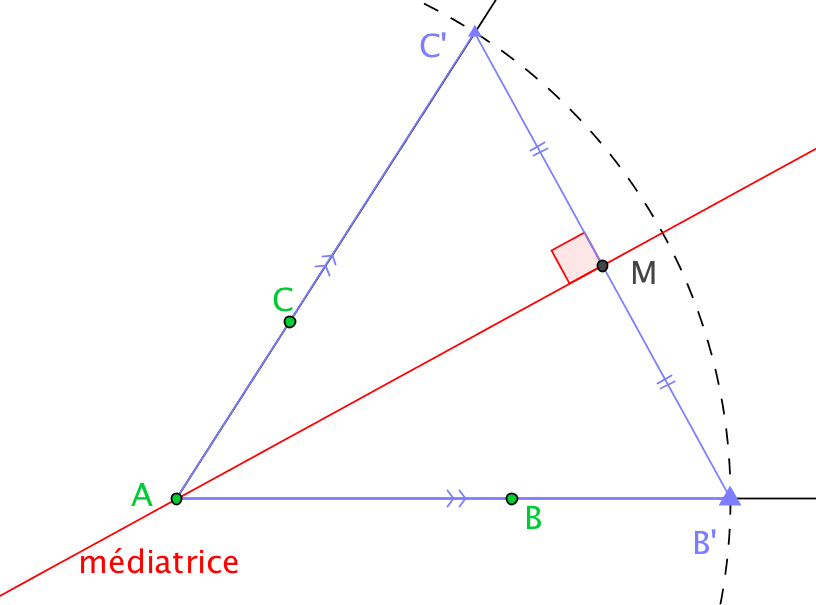Construction de la bissectrice

On en déduit une construction de la bissectrice [ME. VI.1.g]. Il suffit de construire la médiatrice de deux points équidistants de $A$ , sur la figure, les points $B$ et $C'$ .
Déroulez la construction avec les flèches en bas.

Equidistance et bissectrice

Nous démontrons ici le résultat suivant.

La demi-droite

[A x)

est l'ensemble des points de

[\hat{B A C}]

équidistants des demi-droites

[A B)

[A C)

Pour les deux sens de démonstration, nous considérons les projetés respectifs

P

Q

M

sur

[A B)

[A C)

et nous montrons que les triangles

A M P

A M Q

sont isométriques.
Si

M

est un point de la bissectrice

[A x)

, alors les angles

\hat{M A P}

\hat{M A Q}

sont égaux et les triangles sont isométriques par le deuxième cas ; on en déduit

M P = M Q

, c'est-à-dire que

M

est équidistant des demi-droites

[A B)

[A C)

.
Réciproquement si

M

est équidistant des demi-droites

[A B)

[A C)

, alors les deux triangles rectangles ont deux côtés égaux (

M P = M Q

[A M]

commun) donc sont isométriques par le cas des triangles rectangles. Les angles

\hat{M A P}

\hat{M A Q}

sont égaux et

M

appartient à la bissectrice

[A x)

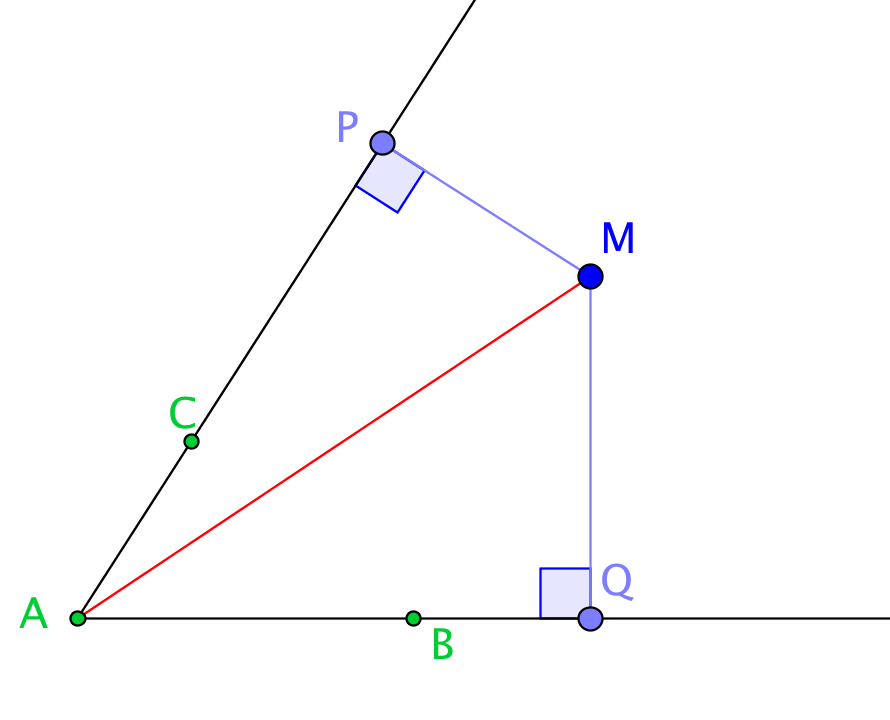Bissectrices dans un triangle

Définition. On appellera bissectrice de l'angle en $A$ dans le triangle $A B C$ la bissectrice de l'angle

\hat{B A C}

Proposition : Soit

A B C

un triangle. Les bissectrices des angles en

A

B

C

sont concourantes en un point omega

équidistant des côtés du triangle, omega

est le centre du cercle inscrit dans

ABC

. Le cercle inscrit est tangent aux côtés de

A B C

Démonstration. Soit $B_{0}$ (respectivement $C_{0}$ ) le point d'intersection de la bissectrice de l'angle en $B$ (resp. en $C$ ) et de $[AC]$ (resp. $[AB]$ ). Ces deux bissectrices se coupent en un point $ω$ , intérieur de $A B C$ , car appartenant à l'intersection des secteurs saillants $[\hat{ABC}]$ et $[\hat{ACB}]$ . Par la propriété 2 des bissectrices intérieures , $ω$ est équidistant d'une part de $[BA)$ et de $[BC)$ (sur la figure $ω F = ω D$ ), d'autre part de $[CA)$ et $[CB)$ (sur la figure $ω E = ω D$ ) donc il est équidistant de $[BA)$ et $[CA)$ (sur la figure $ω F = ω E$ ); on en déduit qu'il appartient à la bissectrice de l'angle en $A$ .
Le cercle centré en $ω$ et passant par les projetés $E$ , $F$ et $G$ de $ω$ sur les côtés du triangle est tangent à ces côtés donc on le dit inscrit dans le triangle.

Modifiez le triangle pour constater que le cercle reste inscrit.

Triangle isocèle

Définition : On dit que le triangle

A B C

est isocèle en $A$ si les côtés

[A B]

[A C]

ont même longueur.

Proposition : Un triangle

A B C

est isocèle en

A

si et seulement si ses angles en

B

et en

C

sont égaux.

Démonstration. Si les côtés $[A B]$ et $[A C]$ ont même longueur, les triangles $A B C$ et $A C B$ sont isométriques par le 3ème cas . On en déduit l'égalité des angles.
Si les angles en $B$ et en $C$ sont égaux, les triangles $A B C$ et $A C B$ sont isométriques par le 2ème cas . On en déduit l'égalité des côtés.

Proposition : Un triangle

A B C

est isocèle en A si et seulement si deux des droites remarquables relatives à

A

sont confondues. Alors elles sont toutes confondues.

Démonstration. On utilise la propriété 2 de la bissectrice et la remarque suivante : Si $A$ appartient à $Δ_{A}$ , la médiatrice de $[B C]$ , alors $Δ_{A}$ est médiane, hauteur.

Détails de la démonstration

Démonstration

La définition d'un triangle isocèle et la propriété (2) de la médiatrice conduisent au résultat suivant.

Lemme : le triangle

A B C

est isocèle en

A

si et seulement

A

appartient à la médiatrice

Δ_{A}

[B C]

Soit $A B C$ un triangle tel que l'un des cas suivants se produit (Faites les figures !):

$Δ_{A}$ est confondue avec la hauteur ou la médiane ou la bissectrice issue de $A$ .
Alors $A$ appartient à la médiatrice et, par le lemme, $ABC$ est isocèle.
La hauteur et la médiane issues de $A$ sont confondues . Alors elles sont confondues avec $Δ_{A}$ puisque perpendiculaires à $[B C]$ en son milieu. Ce cas se ramène au cas 1.
La hauteur et la bissectrice issues de $A$ sont confondues.
Si $P$ est le pied de la hauteur, alors les triangles $A P B$ et $A P C$ sont rectangles, avec un côté commun et un autre angle égal donc isométriques par le 2ème cas . On en déduit l'égalité de $A B$ et $A C$ .
La bissectrice et la médiane issues de $A$ sont confondues.
Soit $I$ le milieu de $[B C]$ , $H$ et $K$ ses projetés respectifs sur $[A B]$ et $[A C]$ . Comme $I$ appartient aussi à la bissectrice de $\hat{A}$ , $I$ est équidistant de $[A B)$ et $[A C)$ , on a donc $I H = I K$ . Les triangles $H I B$ et $K I C$ sont rectangles, avec deux côtés égaux, ils sont isométriques par le cas des triangles rectangles donc les angles $\hat{B}$ et $\hat{C}$ du triangle $A B C$ sont égaux, $A B C$ est isocèle.

Dans tous les cas, le triangle $A B C$ est isocèle. On a donc montré :

Proposition : Un triangle

A B C

est isocèle en A si et seulement si deux des droites remarquables relatives à

A

sont confondues. Alors elles sont toutes confondues.

Droite d'Euler

Proposition : S'ils sont différents, les points

H

O

G

sont alignés sur une droite appelée droite d'Euler du triangle ABC.

Démonstration :

Ce résultat se déduit de la démonstration du concours des hauteurs . En effet, on a obtenu : $H = h (G, - 2) (O)$ . Donc $H$ et $O$ sont alignés avec le centre $G$ de l'homothétie.
Une démonstration niveau collège est suggérée par la figure suivante.

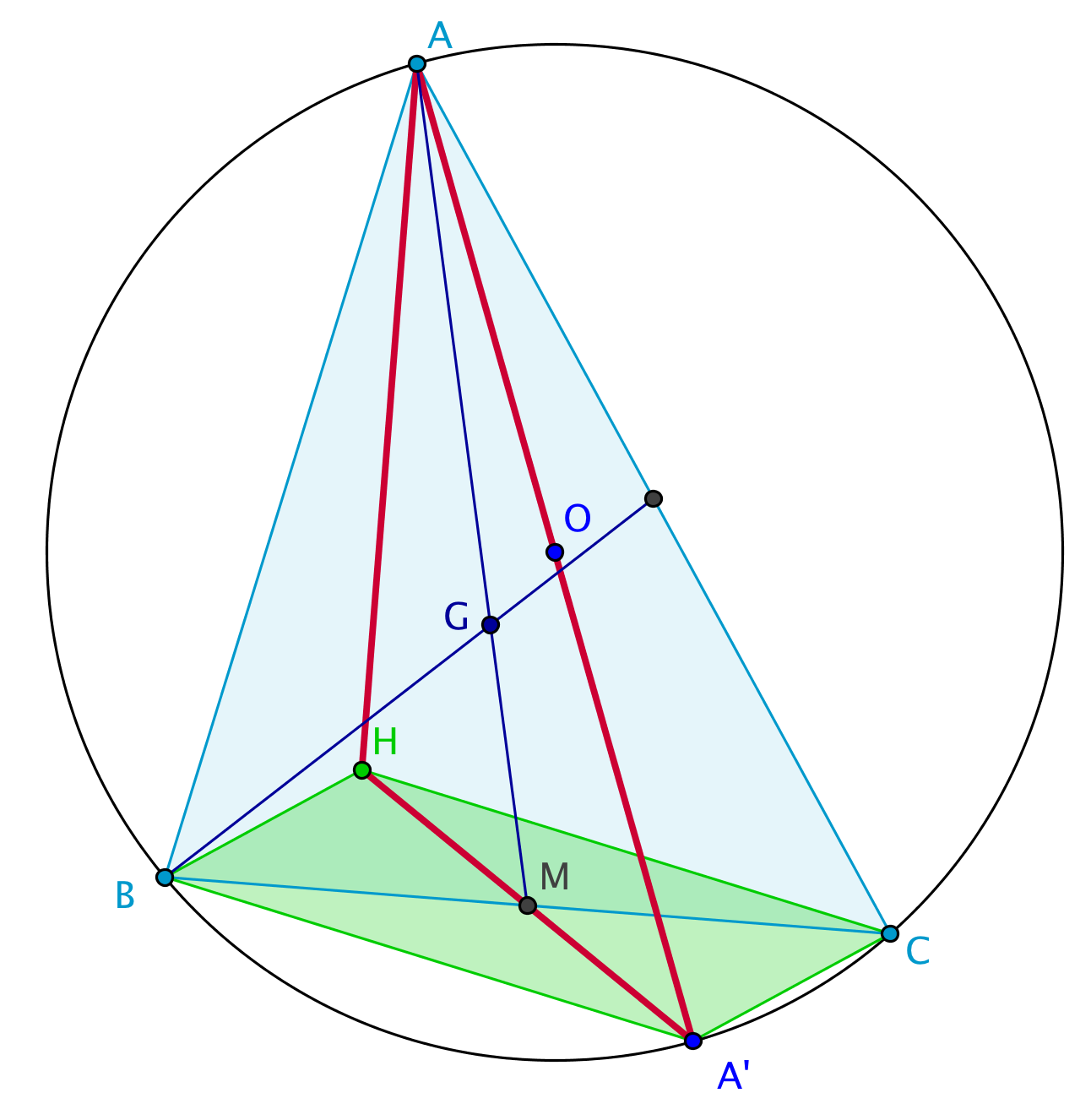
Exercices

Voici quelques exercices sur les droites remarquables.

Reconnaître une droite remarquable sur la figure
Choisir la définition d'une droite remarquable
Donner la définition d'une droite remarquable en lien avec une figure
Tir sur les points de concours des droites remarquables
Définition et position des points de concours des droites remarquables

Vous trouverez d'autres exercices dans la classe ouverte de la licence scientifique générale.

Liste des constructions fondamentales

Les constructions de base présentées dans ce document sont aussi décrites dans [ME.V1.1].

Construction d'une parallèle en 2 pas
Protocole de construction de la médiatrice et du milieu
Construction d'une perpendiculaire
Construction d'un parallélogramme
Report de compas
Image d'un point par une translation
Construction d'une bissectrice

cours : constructions à la règle et au compas, cas d'isométrie ...
: parallelogram, homothétie, translation, symmetry, isometries, triangles, median_line, perpendicular_bisector, altitude, angle_bisector, règle, compas, construction, Euler, CFAI,interactive math, server side interactivity

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.

Droites remarquables, transformations

Sommaire

Préliminaires

Droites remarquables du triangle et transformations

Applications

Cas d'isométrie

Premier cas d'isométrie

Contre-exemple

Les deux triangles sont directement isométriques.

Les deux triangles sont indirectement isométriques.

Deuxième cas d'isométrie

Troisième cas d'isométrie

Cas d'isométrie des triangles rectangles

Constructions à la règle et au compas (principe)

Parallélogramme

Propriétés caractéristiques du parallélogramme

Constructions et parallélogramme

Démonstrations à l'aide de parallélogrammes

Construction d'une parallèle en 2 pas

Droite des mileux

Translation

Symétrie orthogonale

Propriétés

Médiatrice d'un segment

Protocole de construction de la médiatrice et du milieu

Construction d'une perpendiculaire

Homothétie

Homothétie et théorème de Thalès

Médianes

Concours des médianes

Hauteurs

Démonstration avec une homothétie

Relation entre l'orthocentre et le centre du cercle circonscrit

Bissectrice d'un secteur angulaire, d'un angle

Bissectrice d'un secteur [ME.IV.1.j.]

Propriétés de la bissectrice du secteur

Propriétés de la bissectrice intérieure [Ax) du secteur

Construction d'une bissectrice

Construction de la bissectrice

Equidistance et bissectrice

Bissectrices dans un triangle

Triangle isocèle

Démonstration

Droite d'Euler

Exercices

Liste des constructions fondamentales

Propriétés de la bissectrice intérieure $[A x)$ du secteur