Inégalités, inéquations

Objectifs

Majorer, minorer, encadrer, voici les techniques de base de l'analyse et ce cours a pour but de vous présenter ces techniques et de vous y entraîner. Il fournira une approche de la notion de limite. Il s'agit d'un cours d'approfondissement, notamment en ce qui concerne la difficulté des exercices. Il s'adresse à des étudiants post-bac, ayant une certaine pratique des inégalités.

Pour une approche basique des notions d'inégalités, intervalles et encadrements, on consultera avec le plus grand profit du cours DOC Inégalités, intervalles, inéquations .

Sommaire

Encadrements

Voici quelques exercices pour tester vos connaissances et votre pratique des inégalités. Si vous rencontrez des difficultés ou que vous manquiez d'assurance, n'hésitez pas à consulter les parties [A], [B] et [C] du cours Activité inconnue .

Exercices. Ces exercices proposent d'encadrer des expressions en

x

y

connaissant un encadrement des nombres réels

x

y

Encadrement d'une différence
Encadrement de |x|
Encadrement d'un carré
Encadrement d'un produit
Encadrement 1
Encadrement 2
Zone d'inégalité

On rappelle les résultats suivants que l'on cherchera à démontrer pour une meilleure appropriation.

Majoration, minoration des valeurs absolues.

Si $b > 0$ , alors l'inégalité $∣ a ∣ \leq b$ est équivalente à : { $- b \leq a$ ET $a \leq b$ }, c'est à dire : $- b \leq a \leq b$
Si $b > 0$ , alors l'inégalité $∣ a ∣ \geq b$ est équivalente à : { $a \leq - b$ OU $a \geq b$ },

Que se passe-t-il si

b

est strictement négatif ?

Pour le calcul propositionnel, les ET et OU, consultez cette page .

Bornes d'une partie, d'une expression

Avant d'étudier cette page, on consultera, si nécessaire, la page encadrement du cours Activité inconnue .

Définitions. Dans ce cours, on se place dans

ℝ

, ordonné par la relation leq

. Soit

𝒫

une partie non vide de

ℝ

On dit que $𝒫$ est majorée dans $ℝ$ s'il existe un réel $M$ , appelé majorant de $𝒫$ , tel que tous les éléments de $𝒫$ sont inférieurs ou égaux à $M$ .
On dit que $𝒫$ est minorée dans $ℝ$ s'il existe un réel $m$ , appelé minorant de $𝒫$ tel que tous les éléments de $𝒫$ sont supérieurs ou égaux à $m$ .
On dit que $𝒫$ est bornée dans $ℝ$ s'il existe deux réels $m$ et $M$ tels que tous les éléments de $𝒫$ sont supérieurs à $m$ et inférieurs à $M$ .

Exercice 1. Majoration et union

Exercice 2. On considère l'ensemble

A = {(- 1)^{n} + \frac{1}{n^{2}}, n \in ℕ^{*}}

. Quels sont les minorants et les majorants de

A

Tous les réels de : [ $\frac{5}{4}, + ∞$ [ sont des majorants de $A$ . Ceux de : ] - $∞, - 1$ ] en sont des minorants.
On notera que $\frac{5}{4}$ appartient à $A$ , mais que -1 n'y appartient pas.

Exercice 3. On considère l'ensemble

X = {(\frac{1}{p} + \frac{1}{q}), p, q \in ℕ^{*}}

. Quels sont les minorants et les majorants les plus précis de

X

il est facile de voir que $X$ est minoré par 0, et majoré par 2 puisque $p$ et $q$ sont supérieurs ou égaux à 1
Le maximum 2 est atteint pour $p = q = 1$ , c'est donc le meilleur possible (et il appartient à $X$ ).
Si on fait tendre $p$ et $q$ vers $+ ∞$ , on voit que $(\frac{1}{p} + \frac{1}{q})$ tend vers 0, d'aussi près que l'on veut. 0 est donc le meilleur minimum (mais il n'appartient pas à $X$ ).

Majoration sous condition

Exercices. Démontrer les implications suivantes :

$∣ x - 1 ∣ \leq 1 \Rightarrow ∣ \frac{x^{2} \sin x - 2 x}{x^{2} - 6} ∣ \leq 4 .$
Solution
Par hypothèse le réel $x$ est dans l'intervalle $[0; 2]$ , l'expression de la valeur absolue d'un produit et l'inégalité triangulaire nous permettent de majorer le numérateur :
$∣ x^{2} \sin x - 2 x ∣ = ∣ x ∣ ∣ x \sin x - 2 ∣ \leq ∣ x ∣ (∣ x ∣ + 2) \leq 8$
D'autre part le dénominateur $∣ x^{2} - 6 ∣$ vaut $6 - x^{2}$ dans l'intervalle considéré donc est minoré par 2. En combinant ces deux résultats, on obtient l'implication cherchée.
$x \geq 3 \Rightarrow ∣ \frac{x^{2} \exp (- x)}{x^{6} - 20 x^{2}} ∣ \leq \frac{1}{30} .$
Solution
Quand $x$ est positif, exp $(- x)$ est positif et majoré par 1, on obtient donc :
$∣ \frac{x^{2} \exp (- x)}{x^{6} - 20 x^{2}} ∣ \leq ∣ \frac{1}{x^{4} - 20} ∣$
Quand $x$ est supérieur à 3, alors on a $x^{4} \geq 81$ , donc on obtient $x^{4} - 20 \geq 30 > 0$
d'où l'inégalité : $∣ \frac{1}{x^{4} - 20} ∣ = \frac{1}{x^{4} - 20} \leq \frac{1}{30}$ qui permet d'obtenir l'implication
$x \geq 3 \Rightarrow ∣ \frac{x^{2} \exp (- x)}{x^{6} - 20 x^{2}} ∣ \leq \frac{1}{30}$
$∣ x - 2 ∣ \leq 1 \Rightarrow ∣ \frac{\sqrt{∣ x^{2} - 4 ∣}}{x \cos (x - 2)} ∣ \leq 5 \sqrt{∣ x - 2 ∣} .$
Solution
Par hypothèse, si $x \in [1; 3]$ , $x - 2$ est compris entre $- 1$ et $1$ et comme la fonction cosinus est paire et décroissante sur $[0; 1]$ , l'expression $\cos (x - 2)$ est positif et minoré par $\cos (1)$ . De plus $x$ est minoré par $1$ et $x + 2$ est majoré par 5. On obtient donc
$∣ x - 2 ∣ \leq 1 \Rightarrow ∣ \frac{\sqrt{∣ x^{2} - 4 ∣}}{x \cos (x - 2)} ∣ \leq ∣ \frac{\sqrt{x + 2} \sqrt{∣ x - 2 ∣}}{\cos (1)} ∣$ $\leq \frac{\sqrt{5} \sqrt{∣ x - 2 ∣}}{\cos (1)}$
Pour $1 \leq \frac{π}{3}$ , on a : $\cos (1) \geq \frac{1}{2} \geq \frac{1}{\sqrt{5}}$ (on est aussi autorisé à prendre une calculatrice...). Ce qui est équivalent à $\frac{\sqrt{5}}{\cos (1)} \leq 5$ d'où on tire :
$∣ x - 2 ∣ \leq 1 \Rightarrow ∣ \frac{\sqrt{∣ x^{2} - 4 ∣}}{x \cos (x - 2)} ∣ \leq 5 \sqrt{∣ x - 2 ∣}$ .

Limite finie d'une suite

La définition suivante est formellement la même dans $ℝ$ ou $ℂ$ , avec cette différence : la notation $∣ a ∣$ désigne une valeur absolue dans $ℝ$ et un module dans $ℂ$ .

Définition.
Soit

(u_{n})_{n \in ℕ}

une suite numérique, à valeur dans

ℝ

ℂ

. On dit que la suite

(u_{n})_{n \in ℕ}

converge vers le nombre

l

si :

$\forall ε \in ℝ^{} \exists n_{0} \in ℕ$ tel que $\forall n \in ℕ, n \geq n_{0} \Rightarrow ∣ u_{n} - l ∣ \leq ε$

On note alors :

\lim_{n \to + ∞} u_{n} = l

Graphiquement, cela signifie qu'une valeur $ε$ étant fixée, alors au-delà du rang $n_{0}$ (qui dépend du choix de $ε$ ), tous les termes de rang supérieurs à $n_{0}$ sont dans l’intervalle [ $l - ε, l + ε$ ] dans le cas réel, et dans le disque de centre $l$ et de rayon $ε$ dans le cas complexe.

Dans le graphique ci-dessous, pour une suite

u_{n}

convergeant vers 2, on a tracé les points de coordonnée

(n, u_{n})

pour

0 \leq n \leq 20

. On constate que rapidement tous les points se situent à l'intérieur de la bande entre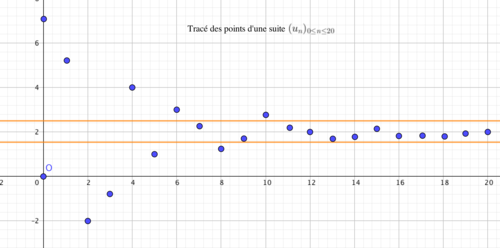

y = 1, 5

y = 2, 5

Exemple. On considère la suite définie par

u_{n} = \frac{2 n^{2}}{n^{2} - 3}, \forall n \in ℕ, n \geq 2

. Montrer avec la définition ci-dessus que la suite tend vers 2.
À partir de quel entier

n_{0}

la quantité

∣ u_{n} - 2 ∣

sera-t-elle inférieure à

ε = 10^{- 2}

Ici, on résout des inéquations : On se donne donc un $ε$ petit dans $ℝ$ et on cherche les $n$ vérifiant $∣ u_{n} - 2 ∣ \leq ε$ : on a les équivalences suivantes
$∣ \frac{2 n^{2}}{n^{2} - 3} - 2 ∣$ $\leq ε \Leftrightarrow \dots \dots \Leftrightarrow (n^{2} \geq \frac{3 ε - 6}{ε} et n^{2} \geq \frac{3 ε + 6}{ε}) \Leftrightarrow n^{2} \geq \frac{3 ε + 6}{ε} \Leftrightarrow n \geq \sqrt{\frac{3 ε + 6}{ε}}$
La valeur $n_{0}$ qui répond à la définition de la limite est la valeur trouvée, mais, comme elle n'est très probablement pas entière, on prendra $n_{0} = E [\sqrt{\frac{3 ε + 6}{ε}}] + 1$ où $E [a]$ est la partie entière de $a$ .
Pour $ε = 10^{- 2}$ , on trouve $n_{0} = 25$ .
On notera que l'on a ici raisonné par équivalence.

On transforme l'expression et on utilise les règles de majoration et minoration d'une fraction :

$∣ \frac{2 n^{2}}{n^{2} - 3} - 2 ∣$ = $∣ \frac{6}{n^{2} - 3} ∣$ = $∣ \frac{6}{(n - \sqrt{3}) (n + \sqrt{3})} ∣$ .

On peut minorer

n + \sqrt{3}

par

n

, puis

n - \sqrt{3}

par 10, ce qui est acquis dès que

n \geq 12

.
On obtient ainsi

∣ \frac{2 n^{2}}{n^{2} - 3} - 2 ∣

\frac{6}{10 n}

Pour

ε = 10^{- 2}

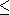
, on trouve

n_{0} = 60

, compatible avec l'hypothèse

n \geq 12

. Ce résultat est moins précis que le résultat précédent mais on a raisonné directement par majoration et minoration ce qui est dans l'esprit de ce document.

Limite infinie d'une suite

Définitions.
Soit

(u_{n})_{n \in ℕ}

une suite à valeur dans

ℝ

On dit que $(u_{n})_{n \in ℕ}$ tend vers $+ ∞$ lorsque $n$ tend vers $+ ∞$ si
$\forall A \in ℝ^{+} \exists n_{0} \in ℕ$ tel que $\forall n \in ℕ, n \geq n_{0} \Rightarrow u_{n} \geq A$
On note alors : $\lim_{n \to + ∞} u_{n} = + ∞$
On dit que $(u_{n})_{n \in ℕ}$ tend vers $- ∞$ lorsque $n$ tend vers $+ ∞$ si
$\forall B \in ℝ^{-} \exists n_{0} \in ℕ$ tel que $\forall n \in ℕ, n \geq n_{0} \Rightarrow u_{n} \leq B$
On note alors : $\lim_{n \to + ∞} u_{n} = - ∞$

Remarque.

Un certain nombre de suites "de référence" tendent vers $+ ∞$ . Par exemple, les suites $(n^{α})_{n \in ℕ}$ (avec $α > 0$ ); $(\ln (n))_{n \in ℕ}$ ; $(\sqrt{n})_{n \in ℕ}$ ; $(e^{n})_{n \in ℕ}$ ... Ces suites seront largement utilisées pour des majorations ou minorations de suites plus complexes, en utilisant les théorèmes de comparaison, voir par exemple un Théorème de comparaison pour les suites .

Exercice. Avec des fonctions trigonométriques

Exercice. Montrer que toutes les suites arithmétiques

(u_{n})_{n \in ℕ}

de raison

r

non nulle tendent vers l'infini.
Même question avec les suites géométriques

(v_{n})_{n \in ℕ}

de raison

q > 1

On peut démontrer par récurrence les formules $u_{n} = u_{0} + n r$ et $v_{n} = v_{0} q^{n}$ .
Pour traiter la suite géométrique, poser $q = 1 + x$ avec $x > 0$ . Commencer à développer à l'aide de la formule du binôme de Newton et minorer judicieusement.

Exercice. On considère la suite

(u_{n})_{n \in ℕ}

définie par la relation de récurrence

u_{n + 1} = u_{n}^{2}

. Que peut-on dire de cette suite dans la cas

u_{0} \in] 0, 1 [

? dans le cas

u_{0} > 1

Théorème de comparaison pour les suites

Cet énoncé résulte facilement de la définition d'une suite tendant vers l'infini.

Théorème.
Soit

(u_{n})_{n \in ℕ}

(v_{n})_{n \in ℕ}

deux suites vérifiant :

Il existe un rang $n_{0}$ tel que pour tout $n \geq n_{0} u_{n} \leq v_{n}$
La suite $(u_{n})_{n \in ℕ}$ tend vers $+ ∞$ .

Alors la suite

(v_{n})_{n \in ℕ}

tend vers

+ ∞

En présence d'une suite

(v_{n})

dont on pense qu'elle tend vers

+ ∞

, on peut chercher à la minorer par une des suites de référence rappelées à la page précédente, ou une suite connue dont on connait le comportement, et on conclura par ce théorème.

Exemple. Déterminer la limite en

+ ∞

de la suite définie par

u_{n} = \frac{e^{n} n^{3}}{2 - \cos (n)} n \geq 1

.
Solution : Cette suite est positive. On minore le numérateur et on majore le dénominateur et on obtient

e^{n} n^{3} \geq e^{n}

2 - \cos (n) \leq 3

. On en déduit une minoration de

u_{n}

par le terme général d'une suite qui tend vers l'infini :

u_{n} \geq \frac{e^{n}}{3}

. Cela démontre l'égalité

\lim_{n \to + ∞} u_{n} = + ∞

Exercice. On considère la suite définie, pour

n \geq 0

, par

u_{n} = \frac{4 n^{2} + 5 n + 2}{2 n + 1}

. Montrer avec la définition ci-dessus, et en utilisant des techniques de majoration/minoration, que cette suite tend vers

+ ∞

Pour rester dans l'esprit du document, on procéde par minoration:
$u_{n} = \frac{4 n^{2} + 5 n + 2}{2 n + 1} = \frac{4 n^{2} + 4 n + 1}{2 n + 1} + \frac{n + 1}{2 n + 1} = 2 n + 1 + \frac{n + 1}{2 n + 1} \geq 2 n + 1$
On se donne un nombre réel $A \geq 0$ et on cherche un entier $n_{0}$ répondant à la définition.
Si on choisit $n$ tel que $2 n + 1 \geq A$ , on peut écrire les inégalités : $u_{n} \geq 2 n + 1 \geq A$ , et en particulier $u_{n} \geq A$ .
il suffit donc de choisit pour $n_{0}$ le plus petit entier naturel $n$ tel que $2 n + 1 \geq A$ , par exemple $n_{0} = E (\frac{A - 1}{2}) + 1$ , où $E (a)$ est la partie entière du réel $a$ .
Ici, nous avons montré que la suite minorante $(2 n + 1)_{n \in ℕ}$ tend vers l'infini et nous avons ainsi conclu avec la définition sans invoquer le théorème.

Exercice. Montrer que la suite définie, pour

n \geq 1

, par

u_{n} = \prod_{k = 1}^{k = 2 n - 1} (2 - \frac{k}{2 n}) = (2 - \frac{1}{2 n}) (2 - \frac{2}{2 n}) (2 - \frac{3}{2 n}) \dots (2 - \frac{2 n - 1}{2 n})

tend vers

+ ∞

Les facteurs correspondants à des valeurs de $k$ comprises entre $1$ et $n$ sont supérieurs ou égaux à $\frac{3}{2}$ . Les autres sont supérieurs à 1, on obtient donc $u_{n} \geq {(\frac{3}{2})}^{n}$ . La suite ${({(\frac{3}{2})}^{n})}_{n \in ℕ}$ est une suite géométrique de raison supérieure à 1, donc elle tend vers $+ ∞$ , ainsi que $(u_{n})_{n \in ℕ}$ , grâce au théorème de comparaison.

Exercice. Comparaison de suites.

Une définition de limite

Définition.

Soit $A$ un sous-ensemble de $ℝ$ et $f$ une fonction définie sur $A$ à valeurs dans $ℝ$ . Soit $b$ un réel (n'appartenant pas nécessairement à $A$ , mais tel que $f$ soit « définie au voisinage de $b$ »), et $L$ un réel.
On dit que $f$ admet $L$ pour limite au point $b$ , lorsque :
Pour tout réel $ε > 0$ , il existe un réel $α > 0$ , tel que, pour tout $x$ dans $A$ avec $∣ x - b ∣ \leq α$ , on ait $∣ f (x) - L ∣ \leq ε$

Cette proposition s'écrit aussi.

$\forall ε > 0, \exists α > 0, [\forall x \in A$ et $∣ x - b ∣ \leq α] \Rightarrow ∣ f (x) - L ∣ \leq ε$

On note $L = \lim_{x \to b} f (x)$ , ou $L = \lim_{b} f$ .

Commentaires sur cette définition

Cette définition de la limite fait appel, on le voit, à des inégalités, ce qui justifie sa présence dans ce document qui, pour autant, n'est pas consacré aux questions de limite.
On notera que la valeur de la limite $L$ est ici supposée connue.

Exercices.

Calcul d'un$epsilon$
Aide visuelle. Le nombre $ε$ étant donné, trouver $α$ en étant aidé visuellement.

En attendant d'avoir des théorèmes sur les limites, on voit que pour démontrer qu'une fonction admet la limite $L$ quand $x$ tend vers $x_{0}$ , on est amené, pour un $ε$ donné, à trouver un nombre $α$ (qui n'est pas unique, bien sûr) vérifiant certaines propriétés. La méthode est décrite à cette page .

Méthode

Une lecture approximative de la définition de la limite peut conduire à une direction de travail peu précise. Certains la réduisent au schéma suivant : si $x$ tend vers $b$ , alors $f (x)$ tend vers $L$ , mettant la priorité au comportement de $x$ , qui va entraîner celui de $f (x)$ . La démarche de la démonstration est exactement inverse.

Revenons à un peu de logique mathématique. Dans une implication $𝒫 \Rightarrow 𝒬$ , le but final est la proposition $𝒬$ , c'est donc ce que l'on doit avoir en perspective dès le début.

On cherche donc à majorer $∣ f (x) - L ∣$ par $ε$ , sous certaines conditions sur $x$ . Pour cela, il peut être très utile de chercher un majorant plus simple de $∣ f (x) - L ∣$ faisant apparaitre la quantité $∣ x - b ∣$ . On vise à obtenir une inégalité du type $∣ f (x) - L ∣ \leq k ∣ x - b ∣$ , avec $k \in ℝ^{+}$ .
Grace à cette inégalité, pour un $ε$ donné et pour obtenir l'inégalité cherchée, il suffit d'avoir $k ∣ x - b ∣ \leq ε$ . Une valeur de $α$ en découle : $α = \frac{ε}{k}$ .
(On notera que cette valeur de $α$ dépend du $ε$ que l'on s'est donné). Ce qui achève la preuve.

On a ainsi trouvé un intervalle $[b - α, b + α]$ sur l'axe des abscisses (et qui doit être dans l'ensemble de définition) dans lequel il suffit de prendre les valeurs de $x$ dans A, pour avoir $∣ f (x) - L ∣ \leq ε$ , c'est à dire pour que que $f (x)$ soit dans l'intervalle $[L - ε, L + ε]$ .

Exemple d'application.

Montrer, en utilisant la définition ci-dessus, que la fonction $f$ définie sur $ℝ$ par $f (x) = x^{2} + 4 x - 5$ admet pour limite 0 lorsque $x$ tend vers $1$ .

Preuve : On note d'abord que le trinôme admet 1 et -5 pour racines. Donc

∣ f (x) - L ∣ = ∣ (x^{2} + 4 x - 5) - 0 ∣ = ∣ x - 1 ∣ ∣ x + 5 ∣

, et on a fait apparaitre la quantité

∣ x - 1 ∣ .

Comme

x

tend vers

1

, on peut supposer que

x

est compris entre

0

2

, mais on introduit donc une condition sur

x

(dont il faudra tenir compte) qui s'écrit

∣ x - 1 ∣ \leq 1

(*).
Comme

x

est compris entre

0

2

5 \leq x + 5 \leq 7

. Cette condition nous permet donc de majorer

∣ x + 5 ∣

par

7

.
Donc

∣ f (x) - L ∣ = ∣ x - 1 ∣ ∣ x + 5 ∣

est majoré par

7 ∣ x - 1 ∣

Soit

ε > 0

, pour que l'inégalité

∣ f (x) - L ∣ \leq ε

soit vérifiée, il suffit que la condition (*) soit vérifiée et qu'on ait

7 ∣ x - 1 ∣ \leq ε

, c'est-à-dire

∣ x - 1 ∣ \leq \frac{ε}{7}

. Donc on choisit

α = \min (1, \frac{ε}{7})

Application. Si on se donne par exemple, $ε = 0, 7$ on obtient $α = 0, 1$ et on sait alors que toutes les valeurs de $x$ se trouvant dans l'intervalle $[0, 9; 1, 1]$ ont des images par $f$ dans l'intervalle $[- 0, 7; 0, 7]$ .

Un exemple simple

Exercice 1. Soit

a

b

des réels,

C

un réel positif, et

n

un entier naturel. Donner une majoration raisonnable de

∣ f (x) - b ∣

de la forme

C ∣ x - a ∣^{n}

$f (x) = x^{3}, a = 2, b = 8$ avec la condition $∣ x - 2 ∣ \leq 1$ .
Solution

$∣ x^{3} - 8 ∣ = ∣ (x - 2) (x^{2} + 2 x + 4)$ $∣ \leq ∣ x - 2 ∣ (x^{2} + ∣ 2 x ∣ + 4)$
Si la condition $∣ x - 2 ∣ \leq 1$ est vérifiée, $x$ est majoré par $3$ et on peut écrire :
$∣ f (x) - b ∣ \leq 19 ∣ x - 2 ∣$
$f (x) = \frac{x^{2} + 3}{x - 2}, a = 1, b = - 4$ avec la condition $∣ x - 1 ∣ \leq \frac{1}{2}$
Solution

$∣ \frac{x^{2} + 3}{x - 2} + 4 ∣ = ∣ \frac{(x - 1) (x + 5)}{x - 2} ∣$
Si $x$ est compris entre 1/2 et 3/2, (on est alors sûr que la fonction est définie), on minore $∣ x - 2 ∣$ par $\frac{1}{2}$ (faire un dessin sur la droite réelle en plaçant $\frac{1}{2}$ , $1$ , $\frac{3}{2}$ et 2, et on majore $∣ x + 5 ∣$ par $\frac{13}{2}$ . On peut donc écrire que
si x est compris entre 1/2 et 3/2 , $∣ \frac{x^{2} + 3}{x - 2} + 4 ∣ \leq 13 ∣ x - 1 ∣$
$f (x) = x^{2} + \frac{1}{x^{2}}, a = 1, b = 2$ avec la condition $∣ x - 1 ∣ \leq \frac{1}{2}$
Solution
$∣ x^{2} + \frac{1}{x^{2}} - 2 ∣$ = $∣ \frac{(x^{2} - 1)^{2}}{x^{2}} ∣$ = $∣ \frac{(x - 1)^{2} (x + 1)^{2}}{x^{2}} ∣$
La fonction est définie si et seulement si $x$ n'est pas nul, nous allons donc supposer que $x$ est entre $\frac{1}{2}$ et $\frac{3}{2}$ , alors $(x + 1)^{2}$ est majoré par $\frac{5^{2}}{2^{2}}$ et $∣ x^{2} + \frac{1}{x^{2}} - 2 ∣$ est majoré par $7 (x - 1)^{2}$ pour faire simple.

Exercice 2. Montrer, avec la définition précédente que

\lim_{x \to 1} (x^{2} + 1) = 2

Solution

∣ f (x) - L ∣ = ∣ (x^{2} + 1) - 2 ∣ = ∣ x - 1 ∣ ∣ x + 1 ∣

.
Au voisinage de 1, on peut supposer que

\frac{1}{2} \leq x \leq \frac{3}{2}

, et donc que

∣ x - 1 ∣ \leq \frac{1}{2}

(*) condition qui sera réutilisée. De plus

\frac{3}{2} \leq x + 1 \leq \frac{5}{2}

On a donc obtenu :

∣ f (x) - L ∣ = ∣ x - 1 ∣ ∣ x + 1 ∣ \leq \frac{5}{2} ∣ x - 1 ∣

Soit

ε > 0

, pour que l'inégalité

∣ f (x) - L ∣ \leq ε

soit vérifiée, il suffit que la condition (*) soit vérifiée et qu'on ait

\frac{5}{2} ∣ x - 1 ∣ \leq ε

, c'est-à-dire

∣ x - 1 ∣ \leq \frac{2 ε}{5}

.
On choisit donc

α = \inf (\frac{2 ε}{5}, \frac{1}{2})

Conclusion :

\forall ε > 0, \exists α > 0 (α = \inf (\frac{2 ε}{5}, \frac{1}{2})) ∣ x - 1 ∣ \leq α \Rightarrow ∣ (x^{2} + 1) - 2 ∣ \leq ε

. Ce qui prouve le résultat cherché.

Exercice 3. Soit

ε

un réel strictement positif. Dans chacun des cas traités au-dessus, proposer une valeur de

α

dépendant de

ε

telle que l'implication suivante soit vraie :

$∣ x - a ∣ \leq α \Rightarrow ∣ f (x) - b ∣ \leq ε$

Solution

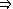
$∣ x - a ∣ \leq α$ Rightarrow $∣ f (x) - b ∣ \leq ε$

Une infinité de choix de

α

sont possibles, le choix dépend de la majoration qu'on a réussi à faire. Les majorations proposées permettent d'affirmer que les valeurs de

α

suivantes conviennent ainsi que toute valeur inférieure.

$α = \inf (\frac{ε}{19}, 1)$ . On doit choisir $α$ inférieur à 1 car la majoration n'est démontrée que pour $∣ x - 2 ∣ \leq 1$ .
$∣ x - 2 ∣ \leq \inf (\frac{ε}{19}, 1)$ ) $∣ x^{3} - 8 ∣ \leq ε$
$α = \inf (\frac{ε}{13}, \frac{1}{2})$ .
$∣ x - 1 ∣ \leq \inf (\frac{ε}{13}, \frac{1}{2}) \Rightarrow$ $∣ \frac{x^{2} + 3}{x - 2} + 4 ∣ \leq ε$
$α = \inf (\frac{\sqrt{ε}}{4}, \frac{1}{2})$ .
$∣ x - 1 ∣ \leq \inf (\frac{\sqrt{ε}}{4}, \frac{1}{2}) \Rightarrow$ $∣ x^{2} + \frac{1}{x^{2}} - 2 ∣ \leq ε$

document donnant une introduction à la notion de limite.
: limit,epsilon,inequalities,inequations, functions,sequence, CFAI,interactive math, server side interactivity

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.

Inégalités, inéquations

Objectifs

Sommaire

A. Inégalités. Encadrements. Inéquations

B. Implication entre inégalités

C. Applications aux limites.

Encadrements

Bornes d'une partie, d'une expression

Majoration sous condition

Limite finie d'une suite

Limite infinie d'une suite

Théorème de comparaison pour les suites

Une définition de limite

Commentaires sur cette définition

Méthode

Un exemple simple