OEF vector subspaces
--- Introduction ---
This module gathers for the time being 8 exercises on
subspaces of vector spaces.
Dimension of intersection
Fill-in: Let F be a vector space of dimension , and let
,
be two vector subspaces of F, of dimensions respectively and . Then
is at least
and at most
.
Dim subspace by system
Let E be a sub-vector space of R defined by a homogeneous linear system. This system is composed of equations, and the rank of the coefficient matrix of this system is equal to . What is the dimension of E?
Dimension of sum
Fill-in: Let F be a vector space of dimension , and let
,
be two vector subspaces of F, of dimensions respectively and . Then
is at least
and at most
.
Subbase
Fill-in: let F be a vector space of dimension , and let B be a basis of F. Let
be a subset of de elements, and let E be the vector subspace of F generated by
. Then dim(E) is
equal to
.
Subbase II
Fill-in: let F be a vector space of dimension , and let B be a basis of F. Let
and
be two subsets of B, with respectively and elements. Suppose that
has elements. Let
and
be the vector subspaces of F generated respectively by
and
, and let
.
Then
is
equal to
.
Dimension of subspace
Fill-in: Let E be a vector subspace of 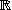 . Then dim(E) is
equal to
.
. Then dim(E) is
equal to
.
Dim subspace of matrices
Fill-in: let M× be the vector space over 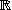 of × matrices, and let E be the vector subspace of M× consisting of matrices A such that =0, where B is a fixed non-zero matrix of dimension ×. Then dim(E) is at least
, and at most
.
of × matrices, and let E be the vector subspace of M× consisting of matrices A such that =0, where B is a fixed non-zero matrix of dimension ×. Then dim(E) is at least
, and at most
.
Extension of subspace
Let F be a vector space of dimension , E a subspace of F generated by a set S, with
. Let v be a vector of F which a linear combination of vectors in S, and let
be the vector subspace of F generated by
. What is the dimension of
?
The most recent version
This page is not in its usual appearance because WIMS is unable to recognize your
web browser.
Please take note that WIMS pages are interactively generated; they are not ordinary
HTML files. They must be used interactively ONLINE. It is useless
for you to gather them through a robot program.
- Description: collection of exercises on vector subspaces. interactive exercises, online calculators and plotters, mathematical recreation and games, Pôle Formation CFAI-CENTRE
- Keywords: CFAI,interactive math, server side interactivity, algebra, linear algebra, vector space, subspace, base, dimension, linear system
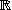 . Then dim(E) is
equal to
.
. Then dim(E) is
equal to
.
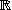 of × matrices, and let E be the vector subspace of M× consisting of matrices A such that =0, where B is a fixed non-zero matrix of dimension ×. Then dim(E) is at least
, and at most
.
of × matrices, and let E be the vector subspace of M× consisting of matrices A such that =0, where B is a fixed non-zero matrix of dimension ×. Then dim(E) is at least
, and at most
.